Python爬取Steam游戏评论 + 游戏基本信息用于数据分析练习。
5.23 突然想到或许可以用群机器人收集反馈群里的数据欸。
爬取数据结构:
1 | - PySteam |
分析思路@
1 | - PySteam |
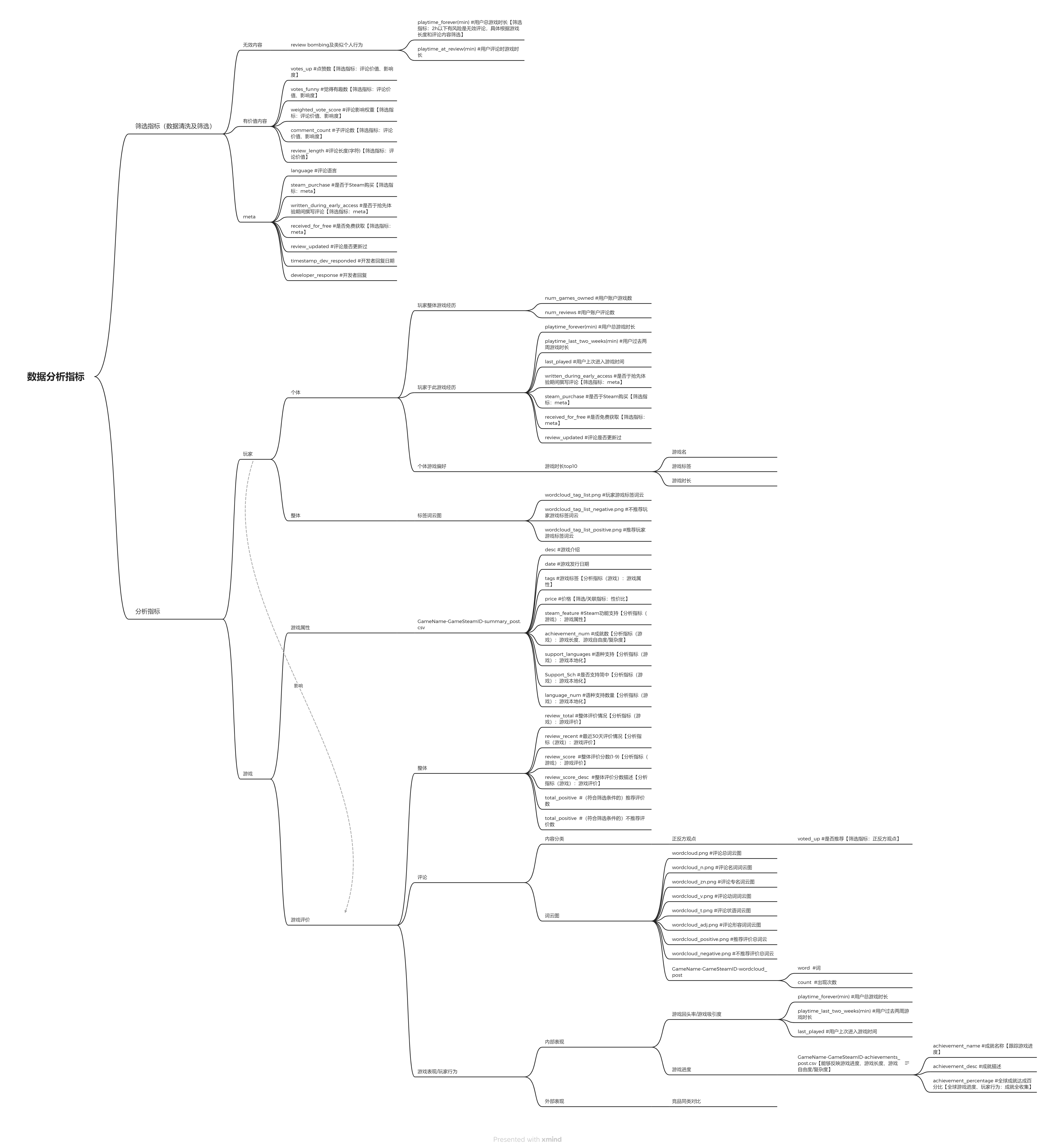
词云示意图:
Python + BeautifulSoup + 单网页(不涉及自动化浏览器翻页)爬虫@
1 | from bs4 import BeautifulSoup |
如果报错lxml,安装 pip install lxml.
1 | headers = { |
函数@
一个html中有各种HTML标签:html、head、body、div、p、a、ul(列表)、li(列表子类)等。
首先是查找定位函数@
page.a@
用法:page.a,page.div等。
功能:只返回第一次出现该标签的内容,范围是<a> ~ </a>
page.find(‘a’,id=’random_id’)@
用法:
page.find('a'),page.find('div')等。page.find('a',id='random_id')或page.find('div',class_='random_id')/page.find(attrs={'class':'random_id'})
功能:
只返回第一次出现该标签的内容,范围是
<a> ~ </a>,此用法同page.a;page.find('a',id='random_id')或page.find('div',class_='random_id'),id标签定位:1
2
3
4
5
6
7
8
9page=```
<a href="http://www.random.url" id="random_id">random_text</a>
<div class="random_id">random_text2</div>
```
page.find('a',id='random_id')
》 <a href="http://www.random.url" id="random_id">random_text</a>
page.find('div',class_='random_id')
》 <div class="random_id">random_text2</div>
page.find_all()@
用法:
page.find_all('a'),page.find_all('div')等单个指定标签page.find_all('a')[0],page.find_all('div')[1]获取列表元素page.find_all(['a','ul','li','div'])多个指定标签正则表达式
1
2
3
4
5
6
7
8
9
10
11
12
13
14import re
page.find_all(re.compile('^a')) #全部以a开头的标签
<a href="/book/1111/">text1</a>
<a target="_blank">text2</a>
<a>text3</a>
page.find_all('a',href=re.compile('^/book'),target='_blank') #获取结果见下
<a href="/book/1111/" target="_blank">text1</a>
<a href="/book/1112/" target="_blank">text2</a>
<a href="/book/1313/" target="_blank">text3</a>
<a href="/book/1154/" target="_blank">text10</a>
<a href="/book/1115/" target="_blank">text15</a>
功能:返回指定标签下所有内容,且是列表list的形式。查看某一元素<div class="random_id">random_text2</div>时需要用[0]标注。
page.select()@
用法 & 功能:
- 类(class)选择器:
page.select('.random_id'),这个指的是html标签内的class="random_id",返回的是完整的html标签框内容。 - ID选择器:
page.select('#random_id'),这个指的是html标签内的id="random_id",返回的是完整的html标签框内容。 - 标签选择器:
page.select('div'),和find_all效果等同。
高级用法:层级选择器@
单层:
page.select('.random_class > ul > li > a')多层:
page.select('.random_class > ul a'),其中使用空格跨过li标签原始html:
1
2
3
4
5
6
7
8
9
10
11<div class="random_class">
<ul>
<li><a title="random_id">list1</a></li>
<li><a>list2</a></li>
<li><a>list3</a></li>
<li><a alt="ramdom">list4</a></li>
<li><a>list5</a></li>
<li><b>list5</b></li>
<li><i>list5</i></li>
</ul>
</div>返回结果:
1
2
3
4
5<li><a title="random_id">list1</a></li>
<li><a>list2</a></li>
<li><a>list3</a></li>
<li><a alt="ramdom">list4</a></li>
<li><a>list5</a></li>
然后是提取(文本)函数@
用法:
- 定位函数+提取函数
- 定位函数(列表)[n] + 提取函数
.text@
获取标签全部文本内容
.get_text()@
获取标签全部文本内容
.string@
获取标签直系文本内容
获取属性标签文本:[‘random_tag’]@
1 | <a random_tag="random_text" class="random_class">text</a> |
page.select(‘.random_class’)[‘random_tag’]
结果:’random_text’
page.find_all(‘a’)[‘random_tag’]
结果:’random_text’
Steam数据挖掘学习@
还有个SteamSpy可以关注下。
整体评价@
9个档位,根据推荐与不推荐的比例,分别是overwhelmingly positive / very positive / positive / mostly positive / mixed / mostly negative / negative / very negative / overwhelmingly negative:
95 - 99% : Overhwelmingly Positive
94 - 80% : Very Positive
80 - 99% + few reviews: Positive
70 - 79% : Mostly Positive
40 - 69% : Mixed
20? - 39% : Mostly Negative
0 - 39% + few reviews: Negative
0 - 19% : Very Negative
0 - 19% + many reviews: Overwhelmingly Negative
src:fixing-steam-s-user-rating-charts
标签@
因为游戏策划需求,在Steam Tag学习专门做了个Steam 标签的分类整理。可以去那里看看。
标签:Steam 上有数百个已批准的标签,因此决定哪些标签对您的游戏来说最合适可能会有些困难。 我们设计了标签向导来帮助您完成这一流程。
标签向导会根据类型、视觉元素与视角、主题与气氛、特色、玩家支持等分类帮助您选出一系列的相关标签。 随着向导越来越了解您的游戏,它会根据 Steam 上相似产品的共同点来突出显示可能相关的标签。 标签向导会帮助您创建标签资料,包括:
类型:
尤其会注意找出最精确的类型或子类型
- 示例:Super Meat Boy 最精确的描述为“精确平台游戏”
- 子类型:动作
- 类型:平台游戏
- 子类型:精确平台游戏
视觉属性:
如:
- 维度:2D、2.5D、3D
- 视角:第三人称、第一人称、俯视、等角视角、横向滚屏等
- 视觉风格:像素图形、拟真、抽象、动漫、可爱、风格化、极简主义等
主题与气氛:
如:
- 主题:科幻、奇幻、太空、僵尸、吸血鬼等
- 气氛:放松、欢乐、氛围等
特色:
如:
- 游戏玩法机制如选择取向、资源管理、贸易等
- 设计材料如物理、程序生成等
- 玩家活动如航海、采矿、黑客等
一些思考和吐槽:
产品设计和游戏设计区别:产品(尤其是功能向产品)适用于某一功能场景,目的是在用户进入某一功能场景范围时能够抓住用户;但游戏并无严苛的功能场景,目的是在用户闲暇时间抓住用户。用户因为闲下来而去打开某个快递软件浏览的可能性远小于其打开游戏类产品。
例外:资讯类功能产品/社交类功能产品,这些都属于basic needs的休闲娱乐范畴。
越来越多的产品加入了游戏元素/模块
review bombing本质上就是一个人的自我展现欲望失控,然后失去理智判断的反常行为,不应该计入数据库:)
数据分析基本概念:@
Ref:SPSSAU
- 定量:数字有比较意义,比如数字越大代表满意度越高,量表为典型定量数据。
- 定类:数字无比较意义,比如性别,1代表男,2代表女。
独立样本 vs. 配对样本@
独立样本:某人A(年龄a,学历b)的成绩x,与另一人B(年龄c,学历d)的成绩y
配对样本:一般是对照实验中出现较多。药物效果x,与药物量y(x,y);某人A在时间a的成绩x(a,x),与某人A在时间b的成绩y(b,y),此时将(a,y)配对是无意义的。
p 值:显著性值或Sig值,描述某事情发生的概率、或有显著差异(默认H0 = 假设无差异,p 值小于0.05,拒绝原假设,因此认为差异有统计学意义)@
H0假设一定是假设观察频数和期望频数一致、相同、无差异、无关。只有这样,才能从观察值,计算出期望值。从而检验观察值和期望值的差距。如果直接假设观察频数和期望频数不一致,不同,相关。那么将无法计算期望值。
如果p 值小于0.01即说明某件事情的发生至少有99%的把握,如果p 值小于0.05(并且大于0.01)则说明某件事情的发生至少有95%的把握。
举例:研究人员想研究不同性别人群的购买意愿是否有明显的差异,如果对应的p 值小于0.05,则说明呈现出0.05水平的显著性差异,即说明不同性别人群的购买意愿有着明显的差异,而且对此类差异至少有95%的把握,绝大多数研究均希望p 值小于0.05,即说明有影响,有关系,或者有差异等。
特别提示@
常见标准:0.01和0.05,分别代表某事情发生至少有99%或95%的把握。
语言表述:0.01或0.05水平显著。
符号标示:0.01使用2个
*号表示,0.05使用1个*号表示。标准设置:如果希望更多标准比如p 值小于0.001,可点击头像处进行设置。
量表,通常指李克特量表,测量样本对于某构念(通俗讲即某事情)的态度或看法.大多数统计方法均只能针对量表,比如信度分析,效度分析,探索性因子分析(Exploratory Factor Analysis,EFA)等
理解P值(假设检验中的p):【能够拒绝H0】不是偶然出现(由于H0通常设置的是“数据有规律性,无异常差异”,在正态性检验时p大于0.05则有正态性)
想证明一班的成绩整体比二班好(有显著差异):
那么原假设H0就设为一班二班成绩相同,其中出现的个别成绩有差异,是由于抽样误差所造成的,纯在偶然性,差异数据不具备统计学意义,可以忽略该差异的影响
备择假设H1就设为一班比二班成绩好,其中样本中出现的一班二班成绩差异不是偶然出现的,具有高度统计学意义,不可忽略该差异的影响
P:在定义了H0的情况下,代表了由于偶然误差导致的H0不成立的偶然性(碰巧可能性大小)。【人话:因为最终判断结果可能会有一定概率导致“因为偶然误差才导致H0不成立”,如果真的出现了这个现象,判断结果【拒绝H0】就并不真实,而是出错的,因此P值衡量的是“因为偶然误差才导致H0不成立”的出现概率,也就是命题【命题【拒绝H0】并不真实】的出现概率,一般意味着命题【应接受H0】的出现概率,也即【H0不真实】的不真实概率,所以简化来说即H0真实(应接受H0)的概率(置信程度)(但只是因为考虑到拒绝H0更容易出错)
P小,拒绝H0的出错概率就小,所以不能接受H0【人话:H0真实的概率小,拒绝H0】
P大,拒绝H0的出错概率就大,所以要接受H0【人话:H0真实的概率大,接受H0】
因此, 当把显著性水平设定为0.05时,
当P值小于0.05时, 我们认为因为偶然性而造成的成绩差异的概率比较小,该差异具备统计学意义,该差异不是由于偶然性的抽样导致的,而是两组数据之间的差异存在着显著意义,因此无法忽略该差异,不能接受H0。因此拒绝原假设,就可以接受一班成绩比二班好的事实;
若P值比0.05大,就原假设中因为抽样误差而造成的成绩差异的可能性比较高,说明没有足够证据证明一班成绩比二班好,保守起见拒绝备择假设 接受原假设
数据处理@
- 标题修改:对标题进行修改或者删除处理;
- 数据标签:标识定类数据时,数字代表的意义;
- 数据编码:对数字进行组合,比如反向题,数据选项组合等;
- 生成变量:比如多个变量标识 1个变量时,可使用“平均值”,还有其它比如虚拟变量,求和,标准化,中心化,归一化,取对数等 10多种处理。
分析方法选择@
SPSSAU建议:先描述想研究什么,用一句话描述,话里面拆开成X和Y:然后结合X与Y的数据类型,选择对应的分析方法。
| 分析方法 | 功能介绍 | 一句话说明 | 数据类型 |
|---|---|---|---|
| 频数 | 百分比 | 男女比例分别多少 | 定类 |
| 交叉(卡方) | 差异关系 | 不同性别【 X 】人群是否抽烟【 Y 】的差异情况 | X(定类) Y(定类) |
| 描述 | 平均值 | 平均身高,量表数据平均得分等 | 定量 |
| 分类汇总 | 差异关系 | 不同城市的销售额情况 | *X(定类)*【 可选 】 Y(定量/定类) |
| 相关 | 相关关系 | 身高【 X 】和体重【 Y 】有没有关系 | *X(定量)*【 可选 】 *Y(定量)*【 可选 】 |
| 回归 | 影响关系 | 身高【 X 】影响体重【 Y 】吗? | Y(定量) X(定量/定类) |
| 聚类 | 人群分类 | 300个人分成几类? | 定量 |
| 因子 | 浓缩 权重 | 30句话概述成5个关键词(因子) 5个关键词(因子)分别代表30句话的信息比重? | 定量 |
| 主成分 | 浓缩 权重 | 30句话概述成5个关键词(成分) 5个关键词(主成分)分别代表30句话的信息比重? | 定量 |
| 信度 | 可靠性 | 数据真实吗? | 定量 |
| 效度 | 有效性 | 数据有效吗? | 定量 |
| 项目分析 | 区分度 | 设计的量表题目是否有区分度? | 定量(量表题) |
| 熵值法 | 权重 | 研究项的权重比例如何? | 定量 |
| 方差 | 差异关系 | 不同收入【 X 】群体的身高【 Y 】是否有差异? | X(定类) Y(定量) |
| t 检验 | 差异关系 | 不同性别【 X 】群体的身高【 Y 】是否有差异?【 X 仅2个类别比如男和女】 | X(定类) Y(定量) |
| 多重响应(多选/单选-多选/多选-单选/多选-多选) | 百分比 | 多选题的选择比例情况如何 | *X(定类)*【 可选 】 多选题选项 |
| 事后多重比较 | 差异关系 | 不同收入【 X 】群体的身高【 Y 】详细差异情况?【 X 两两组别之间差异对比】 | X(定类) Y(定量) |
| 单样本t 检验 | 差异关系 | 身高是否明显等于1.8 | 定量 |
| 配对t 检验 | 差异关系 | 注射新药和没有注射的两组老鼠,血压一样吗? | 配对1(定量) 配对1(定量) |
| 逐步回归 | 影响关系 | 帮我自动找出影响身高 Y的因素 X | Y(定量) X(定量/定类) |
| 分层回归 | 影响关系 | 身高【 X,分层1】对于体重【 Y】的影响,再加入饮食习惯【 X,分层2】,看看饮食习惯对体重的影响有多严重 | Y(定量) 分层1(定量/定类) 分层2(定量/定类) 分层3(定量/定类) 分层4(定量/定类) |
| 正态性检验 | 正态检验 | 数据正态吗? | 定量 |
| 非参数检验 | 差异关系 | 身高数据不正态时,我想研究收入【 X 】与身高【 Y 】的差异关系 | Y(定量) X(定类) |
| 双因素方差 | 差异关系 | 性别【 X 】和地区【 X 】对于身高【 Y 】的差异 | Y(定量) X(定类,2个) |
| 二元Logit | 影响关系 | 哪些因素【 X 】影响人们是否购买电影票【 Y 】 | Y(定类,2项) X(定量/定类) |
| 多分类Logit | 影响关系 | 哪些因素【 X 】影响人们购买不同类型电影票【 Y 】 | Y(定类,2+项) X(定量/定类) |
| 散点图 | 数据关系 | 身高【 X 】和体重【 Y 】的关系情况,并且区分性别【颜色区分】 | Y(定量) X(定量) 颜色区分(定类) |
| 直方图 | 正态性 | 身高数据是否正态分布 | X(定量) |
| 箱线图 | 数据分布 | 身高数据的分布情况 | X(定量) |
| 词云图 | 数据展示 | 热点城市房价指数展示 | X(定量) 加权项(可选) |
通用方法@
频数@
频数分析用于计算定类数据(比如性别,数字代表类别这类数据)的选择频数和比例,频数分析常用于样本基本背景信息统计,以及样本特征和基本态度情况分析。
| 分析项 | 频数分析说明 |
|---|---|
| 性别 | 数字1代表男,数字2代表女,数字分别表示两个类别;男和女分别的选择百分比多少? |
| 年龄 | 数字1代表20岁以下,数字2代表20~30岁,数字3代表30岁以上;数字代表三个不同类别,三个类别人群的百分比是多少? |
分类汇总(?很陌生不太懂)@
分类汇总用于交叉性研究,结合X的放置情况,以及汇总类型的选择情况,最终涉及四种情况,如下表。
| X的放置情况 | 汇总类型 | 对应方法 |
|---|---|---|
| X(不放置) | 平均值(默认) | 详细的统计指标 |
| X(不放置) | 百分比 | 频数分析 |
| X(放置) | 平均值(默认) | 不同分类项下,详细的汇总项统计指标 |
| X(放置) | 百分比 | 交叉(卡方)分析 |
描述@
| 分析项 | 描述分析说明 |
|---|---|
| 网购满意度 | 数字1代表非常不满意,2代表比较不满意,3代表一般,4代表比较满意,5代表非常满意;则可通过描述分析计算平均得分,描述整体满意情况如何。 |
分析结果表格示例如下(SPSSAU同时会生成折线图/雷达图等):
| 样本量 | 最小值 | 最大值 | 平均值 | 标准差 | 中位数 | |
|---|---|---|---|---|---|---|
| 分析项1 | 198 | 1.57 | 5.00 | 3.43 | 0.76 | 0.76 |
| 分析项2 | 198 | 2.00 | 5.00 | 3.93 | 0.86 | 0.86 |
| 分析项3 | 198 | 2.00 | 5.00 | 3.84 | 0.90 | 0.90 |
| 分析项4 | 198 | 1.00 | 5.00 | 3.32 | 1.01 | 1.01 |
- 描述性分析通常可用于 查看 数据是否有异常(最小值或最大值查看),比如出现-2,-3等异常等。
- 如果多个量表题表示一个维度,可使用“生成变量”的平均值功能。将多个量表题合并成一个整体维度。
同时SPSSAU会输出更多细节指标,如下表:
| 名称 | 方差 | 25分位数 | 中位数 | 75分位数 | IQR | 峰度 | 偏度 |
|---|---|---|---|---|---|---|---|
| A1 | 0.728 | 4.000 | 4.000 | 5.000 | 1.000 | 0.482 | -0.841 |
| A2 | 0.585 | 4.000 | 4.000 | 5.000 | 1.000 | 2.317 | -1.214 |
| A3 | 0.683 | 4.000 | 4.000 | 5.000 | 1.000 | 0.630 | -0.774 |
| A4 | 0.905 | 3.000 | 4.000 | 4.750 | 1.750 | -0.487 | -0.474 |
- 上表格中指标使用情况相对较少,25分位数是指有25%的点低于该值;类似还有中位数代表有50%的点低于该值,75分位数代表有75%的点低于该值。
- IQR等于75分位数 – 25分位数,表示数据集中情况。
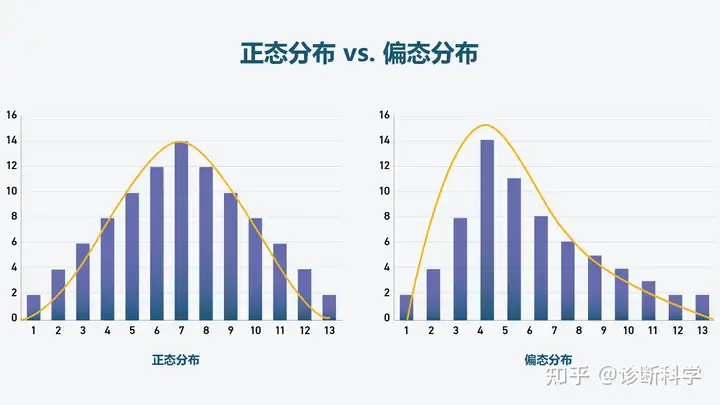
- 峰度和偏度通常用于判断数据正态性情况,峰度的绝对值越大,说明数据越陡峭,峰度的绝对值大于3,意味着数据严重不正态。同时偏度的绝对值越大,说明数据偏斜程度越高,偏度的绝对值大于3,意味着严重不正态(可通过直方图查看数据正态性情况)。
- 除了使用描述性分析外,SPSSAU也建议用户可使用箱线图直观展示数据分布情况。
【对比差异性】卡方分析@
“通用方法”里面默认提供较大样本时最常用的Pearson卡方,医学研究中的卡方检验会提供更多种卡方值指标。
卡方分析(交叉表分析,列联表分析,具体为Pearson卡方),用于分析定类数据与定类数据之间的关系情况.例如研究人员想知道两组学生对于手机品牌的偏好差异情况。
首先判断p 值是否呈现出显著性,如果呈现出显著性,则说明两组数据具有显著性差异,具体差异可通过选择百分比进行对比判断。
卡方值是过程计算值,用于计算p 。卡方值表示观察值与理论值之间的偏离程度。卡方值的大小与样本量(自由度)有关。一般来说,卡方值越大越好,但并不准确。比如5000和5010的差异为10;40和50的差异为10,明显后者差异更大。最终查看卡方值对应的 p 值更准确。
| 分析项 | 卡方检验说明 |
|---|---|
| 学历,网购平台偏好 | 不同学历(本科、高中等)样本人群,他们网购平台(淘宝、京东、拼多多等)偏好是否有差异? |
| 研究性别和是否抽烟之间有没有关系,男性抽烟的比例有没有更高等。 | 性别(男、女)和是否抽烟(是、否)的关系,这一句话里面包含两个词语,分别是:性别,是否抽烟。性别为X,是否抽烟为Y。性别为定类数据,是否抽烟也是定类数据。因而使用卡方分析进行研究。 |

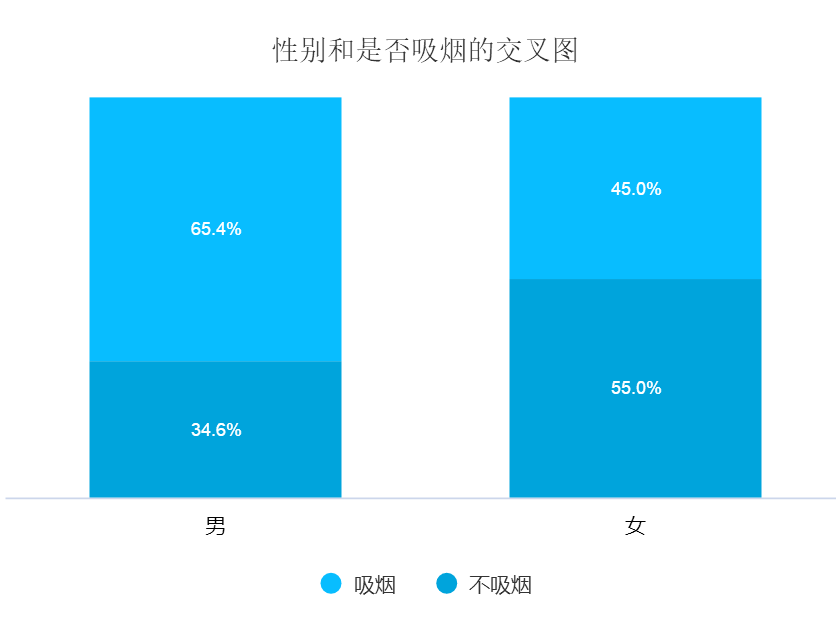
研究性别和是否吸烟之间的关系,由于性别和是否吸烟这两项均为定类数据,因而使用卡方分析进行研究。从上表可知,不同性别群体吸烟情况呈现出显著性差异(χ2=5.734,p =0.017 <0.05),具体通过对比百分比差异可知,男性群体中有65.4%吸烟(明显高于平均水平56.5%),但是女性群体中45%会吸烟。说明男性群体抽烟的比例明显的高于女性群体。
相关分析@
| 分析项 | 相关分析说明 |
|---|---|
| 网购满意度,重复购买意愿 | 网购满意度和重复购买意愿之间是否有关系,关系紧密程度如何? |
相关分析用于研究定量数据之间的关系情况,包括是否有关系,以及关系紧密程度等.此分析方法通常用于回归分析之前; 相关分析与回归分析的逻辑关系为:先有相关关系,才有可能有回归关系。
- 相关分析使用相关系数表示分析项之间的关系;首先判断是否有关系(有*号则表示有关系,否则表示无关系);
- 接着判断关系为正相关或者负相关(相关系数大于0为正相关,反之为负相关);
- 最后判断关系紧密程度(通常**相关系数大于0.4则表示关系紧密)**(也有要求大于0.6的);
- 相关系数常见有两类,分别是Pearson和Spearman,本系统默认使用Pearson相关系数。
| Pearson | 定量数据,数据满足正态性时 | PP/QQ图,直方图均可查看正态性,也或者使用正态性检验(检验最严格); |
|---|---|---|
| Spearman | 定量数据,数据不满足正态性时 | PP/QQ图,直方图均可查看正态性,也或者使用正态性检验(检验最严格); |
| Kendall | 定量数据一致性判断 | 通常用于评分数据一致性水平研究【非关系研究】,比如评委打分,数据排名等。 |
读表:
| 平均值 | 标准差 | 分析项1 | 分析项2 | 分析项3 | 分析项4 | 分析项5 | |
|---|---|---|---|---|---|---|---|
| 分析项1 | 3.43 | 0.76 | 41.4 | 1 | |||
| 分析项2 | 3.93 | 0.86 | .673** | 1 | |||
| 分析项3 | 3.84 | 0.90 | .740** | .712** | 1 | ||
| 分析项4 | 3.32 | 1.01 | .681** | .705** | .642** | 1 | |
| 分析项5 | 3.03 | 1.09 | .520** | .666** | .489** | .604** | 1 |
| ** *p* <0.05 ** *p* <0.01* |
- 如果呈现出显著性(结果右上角有*号,此时说明有关系;反之则没有关系);有了关系之后,关系的紧密程度直接看相关系数大小即可。一般0.7以上说明关系非常紧密;0.4
0.7之间说明关系紧密;0.20.4说明关系一般。 - 如果说相关系数值小于0.2,但是依然呈现出显著性(右上角有号,1个号叫0.05水平显著,2个*号叫0.01水平显著;显著是指相关系数的出现具有统计学意义普遍存在的,而不是偶然出现),说明关系较弱,但依然是有相关关系。
- 相关分析是回归分析的前提条件,首先需要保证有相关关系,接着才能进行回归影响关系研究。
- 因为如果都显示没有相关关系,是不可能有影响关系的。
- 如果有相关关系,但也不一定会出现回归影响关系。
正态性检验@
正态性检验用于分析数据是否呈现出正态性特质。
| 分析项 | 正态性检验说明 |
|---|---|
| 购买意愿 | 样本的购买意愿情况是否符合正态性特质呢? |
正态性特质是很多分析方法的基础前提,如果不满足正态性特质,则应该选择其它的分析方法,SPSSAU将常见的分析方法正态性特质要求归纳如下表(包括分析方法,以及需要满足正态性的分析项,如果不满足时应该使用的分析方法):
| 分析方法 | 说明 | 正态性条件 | 如果不满足,分析方法使用 | 备注 |
|---|---|---|---|---|
| 方差分析 | X对于Y的差异 | Y需要满足正态性 | 非参数检验 | 可考虑对Y进行生成变量转换,比如开根号,自然对数等;希望数据满足正态性 |
| 相关分析 | 分析项相关关系情况 | 分析项均需要正态性 | 如果满足,使用Pearson相关系数,如果不满足使用Spearman相关系数 | 如果不满足正态性,则使用Spearman相关系数 |
| 名称 | 样本量 | Kolmogorov-Smirnov检验 | Shapiro-Wilk检验 | ||
|---|---|---|---|---|---|
| 统计量 | p | 统计量 | p | ||
| 购买意愿 | 17402 | 0.268 | 0.000** | 0.868 | 0.000** |
| * p <0.05 ** p <0.01 |
- 可直接使用“直方图”直观展示数据正态性情况。
- 1:如果样本量大于50,则应该使用Kolmogorov-Smirnov检验结果,反之则使用Shapiro-Wilk检验的结果。
- 2:如果p 值大于0.05,则说明具有正态性特质,反之则说明数据没有正态性特质。
- 3:如果是问卷研究,数据很难满足正态性特质,而实际研究中却也很少使用 不满足正态性分析时的分析方法,SPSSAU认为有以下三点原因:
- 参数检验的检验效能高于非参数检验,比如方差分析为参数检验,所以很多时候即使数据不满足正态性要求也使用方差分析
- 如果使用非参数检验,呈现出差异性,则需要对比具体对比差异性(但是非参数检验的差异性不能直接用平均值描述,这与实际分析需求相悖,因此有时即使数据不正态,也不使用非参数检验,或者Spearman相关系数等)
- 理想状态下数据会呈现出正态性特质,但这仅会出现在理想状态,现实中的数据很难出现正态性特质(尤其是比如问卷数据)【可直接使用“直方图”直观展示数据正态性情况】。
【对比差异性】方差齐检验 & 方差分析@
概念补习:方差越小,数据越稳定。方差(variance)是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。标准差(SD,standard deviation)(是离均差平方的算术平均数(即:方差)的算术平方根,用σ表示。标准差也被称为标准偏差)越小,表明数据越聚集;标准差越大,表明数据越离散。
方差齐检验,用于分析不同定类数据组别 对 定量数据时的波动情况是否一致.例如研究人员想知道三组学生的智商 波动情况是否一致(通常情况希望波动一致,即方差齐)。
- 首先判断p 值是否呈现出显著性(p <0.05),如果呈现出显著性,则说明不同组别数据波动不一致,即说明方差不齐;反之*p* 值没有呈现出显著性(*p* >0.05)则说明方差齐。
| 分析项 | 方差分析说明 |
|---|---|
| 学历,身高 | 不同学历的人群,他们身高波动情况是否有区别? |
分析结果表格示例如下:
| 学历(标准差) | F | p | |||
|---|---|---|---|---|---|
| 本科以下(n=67) | 本科(n=53) | 硕士及以上(n=28) | |||
| 身高 | 1.33 | 0.73 | 0.81 | 3.73 | 0.03* |
| * p <0.05 ** p <0.01 |
- 方差齐是方差分析的前提,如果不满足则不能使用方差分析。
- 方差不齐时可使用‘非参数检验’,同时还可使用welch 方差,或者Brown-Forsythe方差,非参数检验是避开方差齐问题;而welch方差或Brown-Forsythe方差是直面方差齐,即使在方差不齐时也保证结果比较稳健,welch方差和Brown-Forsythe方差仅在计算公式上不一致,目的均是让方差不齐时结果也稳健,选择其中一种即可。
| 类型 | 使用方法 | |
|---|---|---|
| 研究X(定类)对Y(定量)的差异性 | Y方差齐 | 方差分析 |
| 研究X(定类)对Y(定量)的差异性 | Y方差不齐 | 非参数检验或Welch方差或Brown-Forsythe方差 |
方差分析(单因素方差分析),用于分析定类数据与定量数据之间的关系情况.例如研究人员想知道三组学生的智商平均值是否有显著差异.方差分析可用于多组数据,比如本科以下,本科,本科以上共三组的差异;而下述t 检验仅可对比两组数据的差异
- 首先判断p 值是否呈现出显著性,如果呈现出显著性,则说明不同组别数据具有显著性差异,具体差异可通过平均值进行对比判断.
| 分析项 | 方差分析说明 |
|---|---|
| 学历,网购满意度 | 不同学历的人群,他们网购满意度是否有差异? |
| 学历(平均值±标准差) | F | p | |||
|---|---|---|---|---|---|
| 本科以下(n=67) | 本科(n=53) | 硕士及以上(n=28) | |||
| 分析项1 | 3.23±1.33 | 2.88±0.73 | 2.63±0.81 | 3.73 | 0.03* |
| 分析项2 | 2.62±1.48 | 2.57±1.21 | 2.32±0.76 | 0.56 | 0.58 |
| 分析项3 | 2.14±1.10 | 2.16±0.76 | 2.25±0.95 | 0.13 | 0.88 |
| 分析项4 | 3.31±1.12 | 3.32±1.02 | 3.82±0.85 | 2.67 | 0.07 |
| 分析项5 | 3.75±1.06 | 3.56±0.80 | 3.82±0.76 | 0.97 | 0.38 |
| * p <0.05 ** p <0.01 |
【对比差异性】t检验(独立样本t)@
t 检验(独立样本t 检验),用于分析定类数据与定量数据之间的关系情况.例如研究人员想知道两组学生的智商平均值是否有显著差异.t 检验仅可对比两组数据的差异,如果为三组或更多,则使用方差分析.如果刚好仅两组,建议样本较少(低于100时)使用t 检验,反之使用方差分析。
| 分析项 | t 检验说明 |
|---|---|
| 性别,网购满意度 | 不同性别的两类人群,他们网购满意度是否有差异? |
| 性别(平均值±标准差) | t | p | ||
|---|---|---|---|---|
| 男(n=67) | 女(n=53) | |||
| 分析项1 | 3.23±1.33 | 2.88±0.73 | 3.73 | 0.03* |
| 分析项2 | 2.62±1.48 | 2.57±1.21 | 0.56 | 0.58 |
| * p <0.05 ** p <0.01 |
- 首先判断p 值是否呈现出显著性,如果呈现出显著性,则说明两组数据具有显著性差异,具体差异可通过平均值进行对比判断。
方差分析,t 检验和交叉(卡方),共三个分析方法,均是对比差异性。
三个方法的区别如下:
| X数据类型 | X组别 | Y | 分析方法 |
|---|---|---|---|
| 定类 | 2组或者多组 | 定量 | 方差 |
| 定类 | 仅仅2组 | 定量 | t 检验 |
| 定类 | 2组或者多组 | 定类 | 卡方 |
- t 检验一定只能对比两组数据的差异。如果提示“X的组别只能为两组(比如男和女)!”,说明不是2个组别。
- 检查方法为:将X进行频数分析,即可发现X有几个组别。
- 解决办法为:可使用方差分析,也或者将X多个组别组合成两个组别,使用数据编码功能。
单样本t检验@
单样本t 检验用于分析定量数据是否与某个数字有着显著的差异性,比如五级量表,3分代表中立态度,可以使用单样本t 检验分析样本的态度是否明显不为中立状态;系统默认以0分进行对比。
- 首先判断p 值是否呈现出显著性,如果呈现出显著性,则分析项明显不等于设定数字,具体差异可通过平均值进行对比判断。
| 分析项 | 单样本t 检验说明 |
|---|---|
| 网购满意度 | 样本的网购满意度是否明显不为中立状态,以及是否有明显的满意? |
分析结果表格示例如下:
| 样本量 | 最小值 | 最大值 | 平均值 | 标准差 | t | p | |
|---|---|---|---|---|---|---|---|
| 分析项1 | 198 | 1.57 | 5.00 | 3.43 | 0.76 | 3.73 | 0.03* |
| 分析项2 | 198 | 2.00 | 5.00 | 3.93 | 0.86 | 0.56 | 0.58 |
| 分析项3 | 198 | 2.00 | 5.00 | 3.83 | 0.90 | 0.13 | 0.88 |
配对样本t 检验@
配对t 检验,用于配对定量数据之间的差异对比关系.例如在两种背景情况下(有广告和无广告);样本的购买意愿是否有着明显的差异性;配对t 检验通常用于实验研究中。
- 首先判断p 值是否呈现出显著性,如果呈现出显著性,则说明配对数据具有显著性差异,具体差异可通过平均值进行对比判断。
| 分析项 | 配对t 检验说明 |
|---|---|
| 有广告时的购买意愿; 无广告时的购买意愿 | 有广告和无广告两种背景情况下时,购买意愿是否有着显著性差异? |
分析结果表格示例如下:
| 配对(平均值±标准差) | 差值 | t | p | ||
|---|---|---|---|---|---|
| 配对1 | 配对2 | ||||
| 分析项1 配对 分析项2 | 3.23±1.33 | 2.88±0.73 | 0.35 | 3.73 | 0.03* |
| 分析项3 配对 分析项4 | 2.62±1.48 | 2.57±1.21 | 0.05 | 0.56 | 0.58 |
| 分析项5 配对 分析项6 | 2.14±1.10 | 2.16±0.76 | -0.02 | 0.13 | 0.88 |
| * p <0.05 ** p <0.01 |
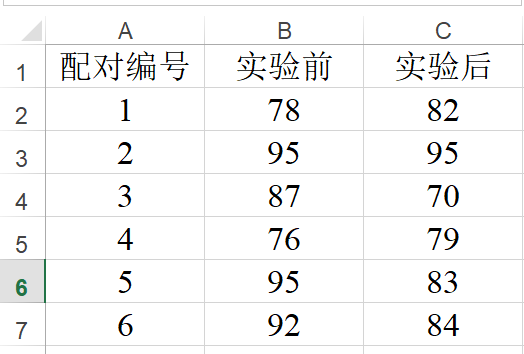
- 配对样本t 检验仅适用于实验研究数据,其余数据并不合适。以及配对样本t 检验时,是以列为单位进行对比。比如下述两列数据进行配对分析。
非参数检验@
非参数检验用于研究定类数据与定量数据之间的关系情况。例如研究人员想知道不同性别学生的购买意愿是否有显著差异。如果购买意愿呈现出正态性,则建议使用方差分析,如果购买意愿没有呈现出正态性特质,此时建议可使用非参数检验。
| 分析项 | 非参数检验分析说明 |
|---|---|
| 性别,购买意愿 | 不同性别人群购买意愿差异情况如何?(如果购买意愿正态则使用方差分析,如果不正态则使用非参数检验) |
分析结果表格示例如下:
| 性别(中位数) | MannWhitney检验统计量 | p | ||
|---|---|---|---|---|
| 男(n=10607) | 女(n=6795) | |||
| 购买意愿 | 3.44 | 3.21 | -16.44 | 0.00** |
| * p <0.05 ** p <0.01 |
- 如果X的组别为两组,比如上表中男和女共两组,则应该使用MannWhitney统计量,如果组别超过两组,则应该使用Kruskal-Wallis统计量结果。SPSSAU自动为你选择MannWhitney或者Kruskal-Wallis统计量。
- 如果p 值小于0.05,但是却出现中位数基本一致没有差异,原因在于数据分布不同所致,此时使用非参数检验将无实际现实意义。SPSSAU建议使用箱线图进行检查,并且建议最终使用方差分析进行差异检验。如果P小于0.05,但是中位数并没有明显的差异,说明差异来源于数据分布不同(而非中位数差异),可使用“箱线图”进行查看。
- 可直接使用“直方图”直观展示数据正态性情况
- 具体来说,如果Z值为正,则意味着第一组样本的中位数大于第二组样本的中位数。反之,如果Z值为负,则意味着第一组样本的中位数小于第二组样本的中位数。
另外,Z值的大小可以反映两组样本之间的差异程度。Z值越大,表示两组样本之间的差异越显著;反之,Z值越小,表示两组样本之间的差异越小。
问卷研究@
信度分析(信度+折半信度+重测信度+折半信度)【量表问卷】@
信度分析用于测量样本回答结果是否可靠,即样本有没有真实作答量表类题项( 重要提示: 信度分析仅仅是针对 量表数据,非量表数据一般不进行信度分析);
信度分析仅针对定量数据. 克隆巴赫信度系数(Cronbach α系数值(一致性内部信度),下同), 如果在0.8以上,则该测验或量表的信度非常好;信度系数在0.7以上都是可以接受;如果在0.6以上,则该量表应进行修订,但仍不失其价值;如果低于0.6,量表就需要重新设计题项。
整体Cronbach α系数值:1.每题项单独进行分析;2.以维度作为单位进行分析,根据问卷提纲,在每一组题针对的维度内进行系数分析
【试问卷】校正的项总计相关性(CITC):此指标用于判断题项是否应该作删除处理,如果值小于0.3,通常应该考虑将对应项进行删除处理;
【试问卷】项已删除的Alpha值(此项删除后的Cronbach α系数值):此指标用于判断题项是否应该作删除处理,如果该值明显高于”α系数”值,此时应该考虑将对应项进行删除处理.
重测信度是指同一批样本,在不同时间点做了两次相同的问题,然后计算两次回答的相关系数,通过相关系数去研究一致性水平。
折半信度是指将所有量表题项分为两半,计算两部分各自的信度以及相关系数,进而估计整个量表的信度。通常心理学、教育学类经典量表常使用折半系数对信度质量衡量。其判断标准可参考α信度系数的衡量标准。
聚类:另一种做法@
还有一种整理问卷的方案是通过聚类,然后各类内进行相关性分析。不知道可不可行。
【经典量表区分性】项目分析(区分度分析)@
项目分析(也称区分度分析);其目的在于研究数据是否可以有效的区分出高低水平。如果一份试卷,所有学生的成绩均在80分,那此份试卷的区分性则很差。如果学生的成绩有高有低,高分学生和低分学生可以很好的区分出来,则说明该试卷有着良好的区分性。
项目分析的原理在于,首先对分析项求和【比如学生语文、数学和英语三科成绩】,然后将求和数据分成三部分(通常是按照百分位数,27%和73%),分别分为低分组,中分组和高分组。低于27%分位数的数据则为低分组,27%~73%之间称为中分组;高于73%则称为高分组。然后使用t 检验去对比低分组和高分组之间是否有着明显的差异,如果具有明显的差异,则说明具有良好的区分性。反之则说明数据区分性差。如果区分性差,则很可能需要将对应的研究项进行删除处理。
对于数据的区分上,通常是按照27%和73%分位数进行拆分;同时也有可能按照25%和75%分位数进行拆分。SPSSAU提供两种拆分方案,在分析完成后,SPSSAU会默认将中间过程涉及的数据,包括求和项,以及分组级别项返回,名称分别类似为:“项目分析****_总分”,“项目分析****_分组级别”。
在问卷量表编制时,基本上均会使用到项目分析,在考试试卷区分上也会使用此方法。除此之外,经典量表的使用时也会用到项目分析。即项目分析通常涉及三个应用场景:
- 经典量表引用时,量表是否具有区分性。
- 设计新量表时,量表题目设计是否具有区分性。
- 考试试卷是否具有区分性。
进阶方法(数据挖掘)【问卷/量表】@
@
聚类分析用于将样本进行分类处理,通常是以定量数据作为分类标准;用户可自行设置聚类数量,如果不进行设置,系统会提供默认建议;通常情况下,建议用户设置聚类数量介于3~6个之间。
- 第一步:进行聚类分析设置
- 第二步:结合不同聚类类别人群特征进行类别命名
| 分析项 | 聚类分析说明 |
|---|---|
| 网购满意度20个题项 | 根据网购满意度情况判定,当前市场上共有几类人群?比如满意度差,一般,满意度高三类人群 |
| 聚类类别 | 频数 | 百分比(%) |
|---|---|---|
| 聚类类别_1 | 82 | 41.4 |
| 聚类类别_2 | 61 | 30.8 |
| 聚类类别_3 | 55 | 27.8 |
| 合计 | 198 | 100.0 |
| 聚类类别(平均值±标准差) | F | p | |||
|---|---|---|---|---|---|
| 类别1(n=82) | 类别2(n=61) | 类别3(n=55) | |||
| 分析项1 | 3.23±1.33 | 2.88±0.73 | 2.63±0.81 | 3.73 | 0.03* |
| 分析项2 | 2.62±1.48 | 2.57±1.21 | 2.32±0.76 | 0.56 | 0.58 |
| 分析项3 | 2.14±1.10 | 2.16±0.76 | 2.25±0.9 | 0.13 | 0.88 |
| 分析项4 | 0.88±0.91 | 3.32±1.02 | 3.82±0.85 | 2.67 | 0.07 |
| 分析项5 | 3.75±1.06 | 3.56±0.80 | 3.82±0.76 | 0.97 | 0.38 |
| 分析项6 | 4.56±0.72 | 4.42±0.61 | 4.57±0.68 | 0.72 | 0.49 |
| 分析项7 | 4.45±0.84 | 4.46±0.66 | 4.55±0.83 | 0.19 | 0.83 |
| 分析项8 | 4.18±0.96 | 4.24±0.67 | 4.36±0.74 | 0.46 | 0.63 |
| * p <0.05 ** p <0.01 |
- 聚类分析的具体聚类方法为K均值聚类;SPSSAU默认将聚类生成的类别保存起来,命名格式为:聚类类别_K均值聚类_,并且结合聚类类别与聚类分析项进行方差分析,并且输出表格。
- 同时SPSSAU会输出聚类项的重要性对比图;在上表格中p 值越小时,说明类别间的差异越大,也即说明对应的该聚类项对于聚类的贡献会越大。正是基于此原理,SPSSAU对于聚类项的p 值进行处理成重要性指标,并且以图形输出。具体聚类项的重要性指标计算公式如下:-log10(p ) / max[-log10(p )];其中p 即为方差分析表格中的p 值,max[-log10(p )]代表-log10(p )的最大值。
@
因子分析(探索性因子分析)用于探索分析项(定量数据)应该分成几个因子(变量),比如20个量表题项应该分成几个方面较为合适;用户可自行设置因子个数,如果不设置,系统会以特征根值大于1作为判定标准设定因子个数。
因子分析通常有三个步骤;第一步是判断是否适合进行因子分析;第二步是因子与题项对应关系判断;第三步是因子命名。
- 第一步:判断是否进行因子分析,判断标准为KMO值大于0.6;
- 第二步:因子与题项对应关系判断。
- 因子与题项对应关系判断:假设预期为3个因子(变量),分析题项为10个;因子与题项交叉共得到30个数字,此数字称作”因子载荷系数”(因子载荷系数值表示分析项与因子之间的相关程度); 针对每个因子(变量),对应10个”因子载荷系数”,针对每个分析项,则有3个”因子载荷系数值”(比如0.765,-0.066,0.093),选出3个数字绝对值大于0.4的那个值(0.765),如果其对应因子1,则说明此题项应该划分在因子1下面.
- 对不合理题项进行删除:共有三种情况; 第一类:如果分析项的共同度(公因子方差)值小于0.4,则对应分析项应该作删除处理;第二类:某分析项对应的”因子载荷系数”的绝对值,全部均小于0.4,也需要删除此分析项;第三类:如果某分析项与因子对应关系出现严重偏差(通常也称作‘张冠李戴’),也需要对该分析项进行删除处理。
- 第三步:因子命名。
在第二步删除掉不合理题项后,并且确认因子与题项对应关系良好后,则可结合因子与题项对应关系,对因子进行命名。
分析项 网购满意度20个题项 因子分析说明 网购满意度由20个题表示,此20个题项可浓缩成几个大方面? 分析结果表格示例如下(SPSSAU同时会生成碎石图):
因子载荷系数 共同度(公因子方差) 因子1 因子2 因子3 分析项1 0.765 -0.066 0.093 0.598 分析项2 0.676 0.081 -0.017 0.464 分析项3 0.657 0.207 -0.205 0.517 分析项4 0.645 0.271 0.089 0.497 分析项5 0.501 0.457 0.085 0.467 分析项6 0.311 0.697 -0.005 0.583 分析项7 0.226 -0.669 0.130 0.516 分析项8 0.191 0.644 0.046 0.453 分析项9 0.476 -0.187 0.542 0.555 分析项10 0.001 -0.048 0.968 0.939 - 因子分析进行因子浓缩时,通常会经历多个重复循环,删除不合理项,并且重复多次循环,最终得到合理结果。
@
主成分分析用于对数据信息进行浓缩,比如总共有20个指标值,是否可以将此20项浓缩成4个概括性指标。除此之外,主成分分析可用于权重计算和综合竞争力研究。即主成分分共有三个实际应用场景:
信息浓缩:将多个分析项浓缩成几个关键概括性指标;
权重计算:利用方差解释率值计算各概括性指标的权重;
综合竞争力:利用成分得分和方差解释率这两项指标,计算得到综合得分,用于综合竞争力对比(综合得分值越高意味着竞争力越强)。
主成分(pca)分析通常有三个步骤;第一步是判断是否适合进行主成分(pca)分析;第二步是主成分与分析项对应关系;第三步是主成分命名.
- 第一步:判断是否进行主成分(pca)分析;判断标准为KMO值大于0.6.
- 第二步:主成分与分析项对应关系判断.
- 特别提示:如果研究目的完全在于信息浓缩,并且找出主成分与分析项对应关系,此时SPSSAU建议使用因子分析【请参考因子分析手册】,而非主成分分析。主成分分析目的在于信息浓缩(但不太关注主成分与分析项对应关系),权重计算,以及综合得分计算。
- 特别提示:有时不太会关注主成分与分析项的对应关系情况,比如进行综合竞争力计算时,不需要过多关注主成分与分析项的对应关系情况。
- **主成与分析项对应关系判断:**假设预期为3个主成分,分析项为10个;主成分与分析项交叉共得到30个数字,此数字称作“载荷系数”(载荷系数值表示分析项与主成分之间的相关程度); 针对每个主成分,对应10个”载荷系数”,针对每个分析项,则有3个“载荷系数值”(比如0.765,-0.066,0.093),选出3个数字绝对值大于0.4的那个值(0.765),如果其对应主成分1,则说明此分析项应该划分在主成分1下面.
- 对不合理分析项进行删除,共有三种情况; 第一类:如果分析项的共同度(公因子方差)值小于0.4,则对应分析项应该作删除处理;第二类:某分析项对应的“载荷系数”的绝对值,全部均小于0.4,也需要删除此分析项;第三类:如果某分析项与主成分对应关系出现严重偏差(通常也称作‘张冠李戴’),也需要对该分析项进行删除处理.
- 第三步:主成分命名
- 在第二步删除掉不合理分析项后,并且确认主成分与分析项对应关系良好后,则可结合主成分与分析项对应关系,对主成分进行命名.
分析结果表格示例如下(SPSSAU同时会生成碎石图):
| 载荷系数 | 共同度(公因子方差) | |||
|---|---|---|---|---|
| 主成分1 | 主成分2 | 主成分3 | ||
| 分析项1 | 0.765 | -0.066 | 0.093 | 0.598 |
| 分析项2 | 0.676 | 0.081 | -0.017 | 0.464 |
| 分析项3 | 0.657 | 0.207 | -0.205 | 0.517 |
| 分析项4 | 0.645 | 0.271 | 0.089 | 0.497 |
| 分析项5 | 0.501 | 0.457 | 0.085 | 0.467 |
| 分析项6 | 0.311 | 0.697 | -0.005 | 0.583 |
| 分析项7 | 0.226 | -0.669 | 0.130 | 0.516 |
| 分析项8 | 0.191 | 0.644 | 0.046 | 0.453 |
| 分析项9 | 0.476 | -0.187 | 0.542 | 0.555 |
| 分析项10 | 0.001 | -0.048 | 0.968 | 0.939 |
主成分(pca)分析进行信息浓缩时,可能会经历多次重复循环,删除不合理项,并且重复多次循环,最终得到合理结果。